Tekst ukazał się w „Filozofuj!” 2015 nr 1, s. 34–39. W pełnej wersji graficznej jest dostępny w pliku PDF.
Gdybyśmy się zrzucili i kupili jakieś większe działo i z dystansu starali się trafić w opuszczony przez ludzi Bardzo Brzydki Budynek w Warszawie, moglibyśmy przyjąć różne strategie. Moglibyśmy strzelać „na czuja” i korygować ustawienia naszego działa, dopóki nie zaczniemy trafiać. W ten jednak sposób nie tylko moglibyśmy kogoś skrzywdzić, nie tylko zmarnowalibyśmy trochę pocisków, ale też ryzykowalibyśmy, że policja odkryje lokalizację naszego działa zanim zdążymy przyczynić się do upiększenia krajobrazu Warszawy.
Bardziej rozważne podejście wymagałoby przestudiowania parametrów naszego działa, być może przeczytania instrukcji obsługi i posłużenia się naszą szczątkową wiedzą z zakresu fizyki newtonowskiej, która błąka się nam gdzieś na dnie mózgu od czasu liceum, by obliczyć jak ustawić działo tak, by w możliwie krótkim czasie dokonać możliwie wielu zniszczeń upiększeń. Wyższość podejścia, przynajmniej częściowo teoretycznego, jest oczywista.
Gdy jednak chodzi o rozumowanie, niemal każdy myśli, że jest to umiejętność, która przychodzi naturalnie i przejawia się w nieomylnej intuicji identyfikującej wszystkie własne argumenty jako genialne i dużo cudzych argumentów jako tak głupie, że aż dziwimy się, jak ktoś zdrowy psychicznie mógł się nimi posłużyć. Obraz ten, aczkolwiek piękny, jest – jak większość pięknych obrazów – fałszywy. Zazwyczaj im głupsi jesteśmy, tym bardziej wierzymy w naszą nieomylność.
Poleganie na naszej niewykształconej intuicji w ocenie rozumowań jest właśnie jak strzelanie z działa „na czuja”. W końcu może trafimy do celu, ale będzie to niewydajne, a częstotliwość naszych pomyłek może wyrządzić krzywdę nie tylko innym, ale też nam samym, a im bardziej skomplikowane zadanie, tym większa szansa, że popełnimy błąd. Gdyby tylko istniało coś, co w przypadku rozumowania działa mniej więcej tak jak fizyka w przypadku strzelania z działa…
Klasyczny przykład omylności
Zacznijmy od dość prostego zadania, którego rozwiązanie umyka jednak większości ludzi za pierwszym razem (będzie to nieco urozmaicone tzw. Zadanie Wasona zaprojektowane przez Petera Wasona). Jeżeli Drogi Czytelnik rozwiąże je od razu poprawnie, świetnie, znajduje się pośród około 10% ankietowanych. Jeżeli nie, nie ma się czym przejmować, znajduje się pośród 90% ankietowanych.
Rozważmy następującą sytuację. Spełniło się Twoje życiowe marzenie, dostalaś(eś) pracę jako nadzorca produkcji bezsensownych karteczek w fabryce stowarzyszonej z lokalną wytwórnią żelbetonu.
Karteczki z jednej strony mogą mieć wydrukowane kółko lub prostokącik. Z drugiej strony mogą być czerwone lub żółte (zob. ilustracja 1). Twój przełożony musi iść pilnować żelbetonu, więc zleca Ci kontrolowanie karteczek wypluwanych przez maszynę. Powiada:
Jest tylko jedna reguła: jeżeli kartka ma kółko z jednej strony, to jej druga strona ma być żółta.
Maszyna wypluwa kartki po cztery sztuki. Przez pierwsze 18 tygodni pracy czujesz się bardzo odpowiedzialnie i za każdym razem obracasz wszystkie cztery kartki, żeby sprawdzić, czy reguła ta nie jest złamana, skazując na karę chłosty osobę obsługującą maszynę za każdym razem, gdy odkryjesz błąd.
Po jakimś czasie jednak Twoje ręce pokrywają się pęcherzami – po części od obracania karteczek, po części od machania pejczem dość często. Zaczynasz zastanawiać się, czy ilości pracy nie da się zminimalizować, nie rezygnując jednak z jej przyjemniejszej część, tzn. nie przepuszczając żadnych błędów.
Drogi Czytelniku, przygotuj stoper i spróbuj na następujący problem odpowiedzieć w 30 sekund!
Przychodzisz do pracy i pierwsze cztery karteczki, które maszyna wypluwa, ułożone są w następujący sposób. Pierwsza jest prostokącikiem do góry, druga kółeczkiem, trzecia żółtą stroną, a czwarta czerwoną stroną. Pytanie: które karteczki naprawdę musisz obrócić, żeby poprawnie sprawdzić, czy nie trzeba kogoś wychłostać?
Proszę, Czytelniku, zapisz sobie odpowiedź, która zdążyła Ci przyjść do głowy w 30 sekund.
Równie klasyczny przykład poprawności
Zanim przejdziemy do omówienia właściwej odpowiedzi kontynuujmy naszą historię. Otóż przełożony zorientował się jednak, że czerpiesz nieco za dużo przyjemności z chłostania personelu i zdecydował się Ciebie zwolnić. Na szczęście w ramach obiektywnego konkursu o pracę, po znajomości zostałeś zatrudniony przez Uniwersytet Górnopółkowy w Dużym Mieście do kontrolowania pracowitości studentów.
Twoje zadanie polega na rzeczy następującej. Wchodzisz na dowolne ćwiczenia, rozglądasz się, identyfikujesz studentów, którzy są przemęczeni, i sprawdzasz, czy mają przy sobie zadanie domowe. Twoja przełożona powiada:
Jest tylko jedna reguła: jeżeli student jest przemęczony, to musi mieć zadanie domowe.
Chłostanie leniwych przemęczonych studentów nie jest, niestety, dozwolone. Ale Uniwersytet Górnopółkowy jest na szczęście instytucją nowoczesną i zainstalował w krzesłach osprzęt do kopania studentów prądem za pomocą panelu kontrolnego znajdującego się na pulpicie wykładowcy. Kochana zaś szefowa pozwoliła Ci delikatnie kopać prądem studentów łamiących wyżej podaną regułę. Zacierając więc ręce i śmiejąc się złowieszczo, wbiegasz na ćwiczenia z logiki.
Okazuje się jednak, że studenci, nie wiedzieć czemu, logiką zainteresowani są jedynie w stopniu umiarkowanym i na ćwiczeniach obecne są tylko cztery osoby.
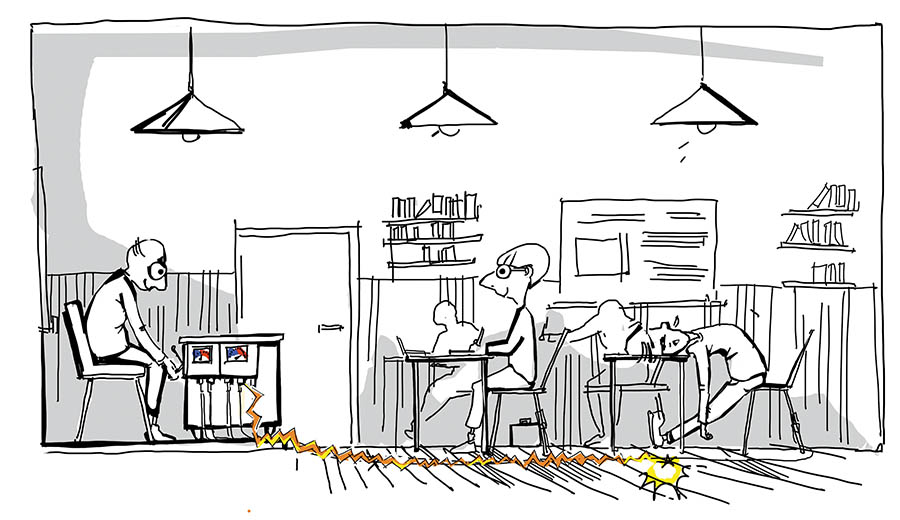
OSOBA 1 – jest rześka.
OSOBA 2 – zdecydowanie jest zaspana.
OSOBA 3 – ma zadanie domowe na wierzchu na stole.
OSOBA 4 – nie jesteśmy pewni, czy jest zaspana, musielibyśmy się lepiej przyjrzeć z bliska, bo usiadła daleko z tyłu, ale na jej stole nie leży nic.
Teraz, drogi Czytelniku, postaraj się odpowiedzieć w trzydzieści sekund. Na które osoby musisz zwrócić uwagę, żeby sprawdzić, czy nikt nie złamał reguły? Ponownie, zapisz sobie swoją odpowiedź i poczekaj na rozwiązanie problemu pod koniec tekstu.
Obiecywanki
Czy da się do problemu podejść w sposób bardziej systematyczny i zmatematyzowany, zamiast strzelać „na czuja”? Tak. Zacznijmy od tego, że obie reguły mają formę „Jeżeli A, to B” (zdania tego typu nazywamy okresami warunkowymi – zdanie A jest tutaj poprzednikiem, a zdanie B następnikiem). Gdybyśmy byli w stanie podać ogólne warunki prawdziwości takich zdań, to może udałoby się je zastosować do rozważanych przed chwilą przykładów. Dobrym źródłem intuicji odnośnie takich warunków prawdziwości jest obiecywanie.
Wyobraźmy sobie, że babcia bardzo ucieszyła się z naszego nowego stanowiska na Uczelni Górnopółkowej. Do tego stopnia, że wolałaby, żebyśmy tę pracę sobie zachowali zamiast spędzać dnie, grając z nią w Resident Evil 5 i przejadając jej emeryturę. Powiada więc:
Jeżeli Cię nie zwolnią przez cały rok, dam Ci moje Playstation.
W jakiej sytuacji byłoby jasne, że babcia nas oszukała? Tylko w jednej: jeżeli poprzednik jest prawdziwy, a następnik fałszywy. Jeżeli pokonamy naszą naturalną chęć podwyższania napięcia w osprzętowaniu i zachowamy pracę przez rok, a babcia nie da nam konsoli, mówiąc, że żartowała, będziemy zdecydowanie mieli prawo konsolę jej po prostu ukraść. W każdym innym przypadku babcia obietnicy nie złamie (nawet jeżeli da nam konsolę, pomimo naszego zwolnienia, bo po prostu nie będzie chciała na nas patrzeć). Wygląda więc na to, że zdania rozważanego typu mają następujące warunki prawdziwości. (Czytelniku, przemyśl sobie wszystkie te przypadki przez chwilę.)
| A | B | Jeżeli A, to B |
| PRAWDA | PRAWDA | PRAWDA |
| PRAWDA | FAŁSZ | FAŁSZ |
| FAŁSZ | PRAWDA | PRAWDA |
| FAŁSZ | FAŁSZ | PRAWDA |
Co z tego?
Dla zagadek rozważanych wcześniej istotne są dwie obserwacje. Po pierwsze, okres warunkowy jest automatycznie prawdziwy, jeżeli jego poprzednik jest fałszywy, niezależnie od tego, czy prawdziwy jest następnik. Po drugie, okres warunkowy jest automatycznie prawdziwy, jeżeli jego następnik jest prawdziwy, niezależnie od tego, czy prawdziwy jest poprzednik.
To jednak znaczy, że w naszych zagadkach, jeżeli wiemy, że warunek wyrażony w poprzedniku nie jest spełniony, możemy danego egzemplarza nie sprawdzać. Dlatego też możemy spokojnie zignorować kwadracik i rześkiego studenta.
Po drugie, jeżeli wiemy, że następnik jest prawdziwy, nie musimy sprawdzać wstępnego warunku. Dlatego możemy spokojnie podarować sobie dalsze sprawdzanie kartki żółtej i studenta posiadającego zadanie domowe. Powinno być teraz jasne, że tak naprawdę przykłady powyższe mają taką samą strukturę logiczną i w obu przypadkach należy sprawdzać tylko element drugi i czwarty. Do wniosku tego doprowadziły w sposób uogólniony rozważania teoretyczne – i w tym sensie skromna aparatura logiczna, którą się posłużyliśmy, prowadzi w sposób prosty i jednolity do poprawnego rozwiązania, w przeciwieństwie do strzelania „na czuja”, które jak wskazują wielokrotne testy, przynajmniej w pierwszym przypadku często zawodzi.
Większość ludzi rozwiązujących powyższe zadania rozwiązuje poprawnie zadanie drugie, ale niepoprawnie rozwiązuje zadanie pierwsze, mimo iż mają one taką samą strukturę. Świadczy to najprawdopodobniej o tym, że im bardziej abstrakcyjne zadanie, tym bardziej zawodna nasza intuicja.
Jeżeli chodzi o rozwój i stosowanie logiki, jest to dopiero bardzo wczesny początek – przykłady i aparatura, którymi się posłużyliśmy, są niezbyt zaawanansowane. Do tematu wrócimy w następnym
numerze.
Rafał Urbaniak – jest logikiem i filozofem. Ukończył studia magisterskie w Gdańsku, doktorat w Calgary, habilitację w Warszawie. Logika go fascynuje i chce się tą odrobiną zrozumienia logiki, jaką posiada, podzielić.
Tekst jest dostępny na licencji: Uznanie autorstwa-Na tych samych warunkach 3.0 Polska. W pełnej wersji graficznej można go przeczytać > tutaj.
Skomentuj