Poniżej znajdują się rozwiązania zagadek logicznych zamieszczonych w naszym dziale Zagadki logiczne. W tym wpisie znajdują się rozwiązania zagadek od #11 do #15.
Zagadka logiczna #11: Demokraci i republikanie
Klub ma 12 członków.
Jeśli oznaczymy początkową liczbę republikanów w klubie jako x i początkową liczbę demokratów w klubie jako y, to informacje zawarte w treści zagadki można przedstawić w postaci układu dwóch równań:
x + 1 = y — 1
2 (x — 1) = y + 1
Stąd możemy obliczyć, że x = 5, a y = 7, a więc całkowita liczba członków klubu x + y = 12.
Zagadka logiczna #12: Czy wyłamiemy się z Matrixa?
Przyjrzyjmy się wpierw drzewku, które przedstawia nasze rozumowanie. Są tu zawarte wszystkie możliwe sposoby, na jakie możemy zaaplikować reguły z naszego zadania (drzewko oczywiście może się ciągnąć w nieskończoność, ale dla uproszczenia przedstawiamy tylko kilka pierwszych kroków). Tak więc w punkcie startowym mamy nasz ciąg MI. W pierwszym kroku możemy dodać do niego albo U albo I. Do ciągu, w którym dodaliśmy U, możemy zastosować tylko regułę 4, przez co otrzymujemy MIUIU, itd. Do ciągu, w którym dodaliśmy I, możemy zastosować regułę 1 (otrzymując MIIU) lub 4 (otrzymując MIIII), itd.
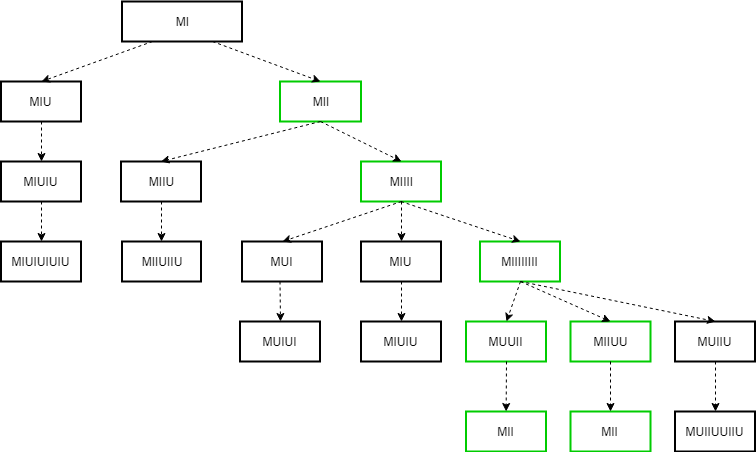
Przeprowadzając takie rozumowanie, w pewnym momencie zauważamy, że nie możemy osiągnąć MU, ponieważ nigdy nie otrzymujemy po M łącznie liczby ‘I’, która byłaby podzielna przez 3. A tylko to pozwoliłoby nam, zgodnie z regułą 2, wyeliminować z ciągu zbędne litery I. Docieramy do tego spostrzeżenia metodą prób i błędów. W pewnym momencie zdajemy sobie sprawę, że „coś tu jest nie tak”. Zmusza nas to do przyjrzenia się samym regułom, którymi się kierujemy, gdy poszukujemy MU. Patrzymy zatem na system z zewnątrz. Program, który będzie działał według tego algorytmu, nie może spojrzeć na swoje reguły z zewnątrz, dlatego będzie szukał tego przekształcenia w nieskończoność.
Zagadka logiczna #13: Większa nieskończoność
Tak, menedżer może przyjąć rezerwację. Nowoprzybyłych gości może ulokować w pokojach na wiele różnych sposobów – tutaj podamy tylko kilka z nich. W najprostszym przypadku, za każdym razem, gdy przybędzie nowy gość, menadżer może poprosić obecnych rezydentów o przeniesienie się do nowego, następnego w kolejności pokoju, a nowoprzybyłemu przydzielić pokój z numerem pierwszym. Jeśli zaś przybędzie na raz nieskończona grupa nowych gości, można poprosić starych gości o przejście do pokoi o numerze będącym dwukrotnością numeru ich poprzedniego pokoju, a nowych ulokować w pokojach o numerach nieparzystych. Można też poprosić starych gości o zajęcie pokoi o numerach będących liczbami pierwszymi, a nowych o zajęcie pokoi o numerach nie będących liczbami pierwszymi.
Zagadka logiczna #14: Kaspar Hauser na rozdrożu
Podobnie jak w poprzedniej zagadce, jest wiele dobrych rozwiązań. Poniżej przedstawiamy jedno z nich.
Można zadać pytanie z alternatywą: powiedz mi Kasparze, czy idziesz z wioski ludzi mówiących prawdę lub wioski ludzi, którzy zawsze kłamią?
Prawdomówny nie może kłamać, zatem odpowie „TAK”, bowiem faktycznie idzie z jednej z tych dwóch wiosek.
Kłamca odpowie „NIE”, ponieważ, gdyby powiedział „TAK”, przyznałby się, że idzie z jednej z tych dwóch wiosek, a zatem powiedziałby prawdę. A przecież kłamca nigdy nie mówi prawdy.
Inne rozwiązanie podane jest w filmie, do obejrzenia którego gorąco zachęcamy ;).
Zagadka logiczna #15: Łowca wampirów
Zdanie wypowiedziane przez Annę jest prawdziwe lub fałszywe.
Jeżeli jest prawdziwe, to obie siostry są rzeczywiście obłąkane. Anna jest więc obłąkana, a jedynym obłąkanym Transylwańczykiem, który może wygłaszać zdania prawdziwe, jest obłąkany wampir. Jeżeli zatem zdanie Anny jest prawdziwe, to Anna jest wampirem.
Załóżmy, że zdanie Anny jest fałszywe. Co najmniej więc jedna z sióstr jest zdrowa. Jeśli zdrowa jest Anna, to skoro wygłosiła zdanie fałszywe, musi być wampirem. A co, jeśli Anna jest obłąkana? Zdrowa wtedy musi być Maria. Maria zatem, wygłosiwszy zdanie sprzeczne z fałszywym zdaniem Anny, wygłosiła zdanie prawdziwe. Maria jest zatem zdrowa i wygłosiła zdanie prawdziwe. Jest więc człowiekiem, a Anna nadal musi być wampirem.
Niezależnie od tego zatem, czy zdanie Anny jest prawdziwe, czy też fałszywe, Anna jest wampirem.























Za demokratów się nie biorę, za bardzo spójna.
Z tym Matrixem … nie da się tego zrobić “metodą na lenia ?”
1. Po I mogę dodać U … i co mi to da ?
2. III można zamienić na U … skąd miałbym niby wytrzasnąć III ?
3. UU mogę usunąć … czyli musiałbym mieć MUUU … jeszcze lepiej.
4. Mogę podwoić … tylko po co ?
Wynika z tego, że nie ma szans na stworzenie samego MUUU, bądź MIII … przynajmniej w jednym ciągu. Kiedyś robiłem tak zadania z matmy, to zawsze były jedynki.
∞
“Nie każdy jednak wie, że zbiór liczb rzeczywistych jest liczniejszy od zbioru liczb naturalnych – jego nieskończoność jest „większa”. ”
Biorąc pod uwagę, że naturalne mogą być tylko całe ? Aha … w sensie 1 2 3 4 … i nie ma tam ułamków, pierwiastków i reszty bzdet ?
A jeśli i tak i nie ? W sensie, jeśli nieskończona jest nasza nieskończoność to jest skończona ale jeśli nieskończoność jest nieskończona to jest nieskończona. Albo inaczej, czy nieskończoność jako pojęcie oznacza liczby, których w danym czasie NIE JESTEŚMY w stanie policzyć, czy może traktujemy to na poważnie że nieskończoność to ciąg liczb, które NIGDY nie będą miały końca. Jeśli to drugie to ten hotel NIE MÓGŁBY istnieć, ponieważ te nieskończenie wiele pokoi musiałoby się rozciągać po całej wolnej przestrzeni kosmicznej, a więc nie mogłyby istnieć ani wszechświaty, ani gwiazdy, ani planety bo całą wolną przestrzeń kosmiczną, planetarną i każdą inną zajmowałyby pokoje hotelowe. Skoro cały wszechświat jest jednym wielkim pokojem hotelowym, to niby gdzie mieli by przybywać nowi goście ? A skoro nie mogą przybyć to jaki jest sens pytania, o liczbę gości którzy przybędą ? Co innego jeśli nieskończoność to liczba, która istnieje ale nie możemy jej pojąć, wtedy jest to możliwe … zaraz, skoro nie znam skończenie wielkiej nieskończoności, to skąd niby mam wiedzieć czy pokoi wystarczy ?
Sierota
Czemu nie ? Przecież ma rację.
Moim zdaniem oczekiwał pytania “Czy możesz kłamać ?” Kłamca (zgodnie z logiką) powie, że może bo ZAWSZE kłamie ale w ten sposób powie prawdę, przez co nie będzie już kłamcą. Na “chłopski rozum” odpowie, że nie bo przecież jest kłamcą. Ale co odpowie ten prawdomówny ? Może odpowiedzieć dosłownie cokolwiek, w oparciu o swoje przekonania.
Wampiry … nie ma się czego przyczepić.